PyTorch 튜토리얼 - 03 신경망(Neural Networks)

PyTorch 튜토리얼 - 03 신경망(Neural Networks)

파이토치 60분 블리츠

원문 링크

• PyTorch 튜토리얼 - 01 텐서(Tensors)
• PyTorch 튜토리얼 - 02 자동미분(autograd)
• PyTorch 튜토리얼 - 03 신경망(Neural Networks)
• PyTorch 튜토리얼 - 04 분류기 학습(Training a classifier)

PyTorch

PyTorch는 다음 두 가지 기능이 구현된 과학 연산을 위한 패키지이다.

1. NumPy를 대신하여 연산 시 GPU 성능을 사용
2. 신경망 구현에 유용한 자동 미분 연산

튜토리얼 목표

• PyTorch의 Tensor 라이브러리 및 신경망에 대한 이해
• 이미지 분류를 위한 신경망 모델 학습

Note torch, torchvision 설치 필요

신경망(Neural Networks)

torch.nn 패키지를 이용하여 신경망을 구축할 수 있다.

이전에 autograd에 대해 살펴 보았었는데, nn은 autograd에 의존하여 모델을 정의하고, 미분을 수행한다. nn.Module은 레이어와 출력을 반환하는 forward(input)메서드를 포함하고 있다.

숫자 이미지를 분류하는 다음 네트워크 예시를 살펴보자.

Convolutional Neural Network

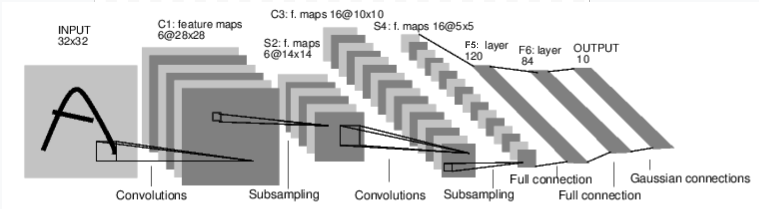
위 예시는 간단한 피드 포워드 네트워크이다. 입력을 받아 여러 레이어를 차례로 통과시킨 다음 마지막으로 출력을 반환한다.

신경망의 일반적인 학습 절차는 다음과 같다.

• 학습 가능한 파라미터(또는 가중치)가 있는 신경망 정의
• 입력 데이터 세트에 대해 반복
• 네트워크를 통한 프로세스 입력
• 손실 계산(정답과의 차이)
• 기울기를 네트워크의 파라미터로 다시 전파
• 일반적으로 간단한 업데이트 규칙을 사용하여 네트워크의 가중치를 업데이트
  • weight := weight - learning_rate * gradient

네트워크 정의

네트워크를 정의해보자.

import torch
import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # 1 input image channel, 6 output channels, 3x3 square convolution
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 3)
        self.conv2 = nn.Conv2d(6, 16, 3)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 6 * 6, 120)  # 6*6 from image dimension
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # If the size is a square you can only specify a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

    def num_flat_features(self, x):
        size = x.size()[1:]  # all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features


net = Net()
print(net)

Net(
  (conv1): Conv2d(1, 6, kernel_size=(3, 3), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(3, 3), stride=(1, 1))
  (fc1): Linear(in_features=576, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

forward함수를 정의하기만 하면 autograd를 사용하여 기울기가 계산되는 backward함수가 자동으로 정의된다. forward함수에서 텐서 연산을 사용할 수 있다.

모델의 학습 가능한 파라미터는 net.parameters()에 의해 반환된다.

params = list(net.parameters())
print(len(params))
print(params[0].size())  # conv1's .weight

10
torch.Size([6, 1, 3, 3])

랜덤한 32x32 입력을 시도해보자. 참고로 LeNet의 예상 입력 크기는 32x32이다. MNIST 데이터 세트에서 이 네트워크를 사용하려면 데이터 세트의 이미지 크기를 32x32로 조정해야한다.

input = torch.randn(1, 1, 32, 32)
out = net(input)
print(out)

tensor([[-0.0604, -0.0616, -0.1291, -0.0600, -0.1000,  0.0464, -0.0559,  0.0095,
         -0.0208,  0.0836]], grad_fn=<AddmmBackward>)

랜덤 기울기들로 모든 파라미터 및 역전파의 기울기 버퍼를 0으로 만든다.

net.zero_grad()
out.backward(torch.randn(1, 10))

요약

• torch.Tensor - backward()와 같은 자동 미분 연산을 지원하는 다차원 배열. 또한, 각 텐서에 대한 기울기를 가지고 있음.
• nn.Module - 신경망 모듈. 파라미터를 GPU로 이동, 추출, 로드하는 것 등을 돕는 파라미터를 캡슐화하는 편리한 방법.
• nn.Parameter - 모듈에 속성으로 할당될 때 파라미터로 자동 등록되는 일종의 텐서
• autograd.Function - autograd 작업의 순방향 및 역방향 정의를 구현. 모든 텐서 연산은 텐서를 만든 함수에 연결하고 기록을 인코딩하는 하나 이상의 Function 노드를 만듦.

지금까지 다룬 것

• 신경망 정의
• 입력 처리 및 역전파 호출

남은 것

• 손실 계산
• 네트워크의 가중치 업데이트

손실 함수(Loss Function)

손실 함수는 (모델 출력값, 타겟 값) 입력 쌍을 가져와 모델 출력값이 타겟 값에서 얼마나 멀리 떨어져 있는지를 추정하는 값을 계산한다.

nn패키지에는 몇 가지 다른 손실 함수들이 있다. 간단한 손실 함수로는 입력과 목표 사이의 평균 제곱 오차를 계산하는 nn.MSELoss가 있다.

예시를 살펴보자.

output = net(input)
target = torch.randn(10)  # a dummy target, for example
target = target.view(1, -1)  # make it the same shape as output
criterion = nn.MSELoss()

loss = criterion(output, target)
print(loss)

tensor(1.0305, grad_fn=<MseLossBackward>)

이제 .grad_fn 속성을 사용하여 역방향 손실을 추적하면 다음과 같은 계산 그래프가 표시된다.

input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
      -> view -> linear -> relu -> linear -> relu -> linear
      -> MSELoss
      -> loss

loss.backward()를 호출하면, 전체 그래프는 각 손실에 대해 미분된다. requires_grad=True인 옵션을 갖는 그래프의 모든 텐서들은 기울기가 축적된 .grad 텐서를 갖게 된다.

예를 들어, 몇 단계를 거슬러 가보자.

print(loss.grad_fn)  # MSELoss
print(loss.grad_fn.next_functions[0][0])  # Linear
print(loss.grad_fn.next_functions[0][0].next_functions[0][0])  # ReLU

<MseLossBackward object at 0x000001B5871A2A90>
<AddmmBackward object at 0x000001B5871A2B38>
<AccumulateGrad object at 0x000001B5871A2A90>

역전파(Backprop)

오류를 역전파하기 위해 우리가 해야할 것은 단지 loss.backward()를 호출하는 것이다. 그럼에도 기존 기울기를 지워야한다. 그렇지 않으면 기울기가 기존 기울기에 누적된다.

이제 loss.backward()를 호출하고, 역전파 전후의 conv1의 편향과 기울기를 살펴 보자.

net.zero_grad()     # zeroes the gradient buffers of all parameters

print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)

loss.backward()

print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)

conv1.bias.grad before backward
tensor([0., 0., 0., 0., 0., 0.])
conv1.bias.grad after backward
tensor([ 0.0022,  0.0045, -0.0037, -0.0004,  0.0041,  0.0095])

이제 손실 함수를 사용하는 방법을 살펴 보았다.

참고 자료
신경망 패키지에는 심층 신경망의 구성 요소를 형성하는 다양한 모듈과 손실 함수가 포함되어 있다. 전체 목록은 여기에 있다.

유일하게 남은 것

• 네트워크의 가중치 업데이트

가중치 업데이트

실제로 사용되는 가장 간단한 업데이트 규칙은 SGD(Stochastic Gradient Descent)이다.

weight = weight - learning_rate * gradient

간단한 파이썬 코드를 이용해 이를 구현할 수 있다.

learning_rate = 0.01
for f in net.parameters():
    f.data.sub_(f.grad.data * learning_rate)

그러나 신경망을 사용할 때 SGD, Nesterov-SGD, Adam, RMSProp 등과 같은 다양한 업데이트 규칙을 사용하고 싶을 수도 있다. 이러한 모든 메서드가 구현된 torch.optim 이라는 패키지를 사용하면 된다. 사용법은 매우 간단하다.

import torch.optim as optim

# create your optimizer
optimizer = optim.SGD(net.parameters(), lr=0.01)

# in your training loop:
optimizer.zero_grad()   # zero the gradient buffers
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()    # Does the update

파이토치 60분 블리츠

원문 링크

• PyTorch 튜토리얼 - 01 텐서(Tensors)
• PyTorch 튜토리얼 - 02 자동미분(autograd)
• PyTorch 튜토리얼 - 03 신경망(Neural Networks)
• PyTorch 튜토리얼 - 04 분류기 학습(Training a classifier)