퀀트용어 - CAGR(연복리수익률)과 MDD(최대손실율)

Compound Annual Growth Rate, Maximum Draw Down

CAGR(Compound Annual Growth Rate)

CAGR은 연복리 수익률을 의미한다. 수익률을 산술평균이 아닌 기하평균으로 계산한다는 점이 중요하다.1,000만 원을 투자해 10년 후 1억 원이 되었다고 할 때, 연복리 수익률은 다음과 같이 구할 수 있다.

\[{CAGR(연복리 수익률)} = {\left(\frac{평가 금액}{투자 금액}\right)}^{\left(\frac{1}{투자년수}\right) - {1}} = {\left(\frac{1억 원}{1,000만 원}\right)}^{\left( \frac{1}{10}\right)}-{1} = 약 25\%\]

즉, 10년의 투자 기간 동안 매년 꾸준히 25% 씩 수익을 냈다면 아래와 같이 1,000만 원이 1억 원으로 불어나는 것을 알 수 있다.

\[{1,000만 원} * {(1 + 0.25)}^{10} = 약 1억 원\]

CAGR의 개념을 활용하면 목표 수익률도 계산해 볼 수 있다. 예를 들어, 1,000만 원을 투자해 3년 후 1,500만 원으로 불리고 싶다면 매년 14.47% 의 수익률을 꾸준히 유지하면 된다.

투자금액 = 1000
투자기간 = 3
목표금액 = 1500

CAGR = (목표금액 / 투자금액) ** (1/투자기간) - 1
print(f"{CAGR*100:.2f}%")

14.47%

혹은 1,000만 원을 투자하여 CAGR 15%를 달성하면 20년 후 자산이 얼마 만큼 불어날지도 알 수 있다. 다음과 같이 계산해보면, 1,000만 원이 20년 후 약 1억 6천만원까지 불어나는 것을 알 수 있다.

투자금액 = 1000
CAGR = 0.15
투자기간 = 20

평가금액 = 투자금액 * (1 + CAGR) ** 20
print(f"{평가금액:,.0f}만 원")

16,367만 원

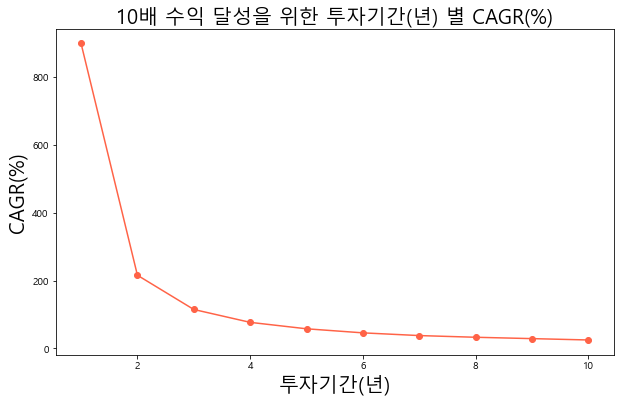
나아가 1,000만 원을 1억 원으로 불리고 싶을 때, 다음과 같이 투자기간에 따른 CAGR을 비교해볼 수도 있다. 1년 안에 1억 원을 만들기 위해서는 CAGR 900%라는 비현실적인 수준을 달성해야 하지만, 투자기간을 10년으로 늘리면 CAGR 25%라는 비교적 현실적인 수준(?)을 달성하기만 하면 된다. 눈으로 확인해도 투자기간이 3년 이상이 되면 목표금액에 달성하기 위해 필요한 CAGR의 수준이 크게 줄어드는 것을 알 수 있다.

import pandas as pd


def CAGR(투자금액, 목표금액, 투자기간):
    return (목표금액 / 투자금액) ** (1 / 투자기간) - 1


투자금액 = 1000
목표금액 = 10000

투자기간목록 = range(1, 11)
CAGR목록 = [int(CAGR(투자금액, 목표금액, 투자기간)*100)for 투자기간 in 투자기간목록]

df = pd.DataFrame({"투자기간(년)": 투자기간목록,
                   "CAGR(%)": CAGR목록})
df.set_index('투자기간(년)').T

투자기간(년)	1	2	3	4	5	6	7	8	9	10
CAGR(%)	900	216	115	77	58	46	38	33	29	25

import matplotlib.pyplot as plt
plt.figure(figsize=(10, 6))
plt.plot(
    df['투자기간(년)'],
    df['CAGR(%)'],
    marker="o",
    color='tomato',
)
plt.title("10배 수익 달성을 위한 투자기간(년) 별 CAGR(%)", fontsize=20)
plt.xlabel(df.columns[0], fontsize=20)
plt.ylabel(df.columns[1], fontsize=20)
plt.show()

MDD(Maximum Draw Down)

MDD는 특정 투자 기간 동안의 낙폭들 중 최대 낙폭값을 고점값으로 나눈 비율로 최대 손실율을 의미한다. 예를 들어, 6개월의 투자 기간 동안 월 별 주가가 100, 110, 105, 115, 105, 110 이었다면, ‘낙폭1‘(110 - 105), ‘낙폭2‘(115 - 105) 중 최대 낙폭값인 ‘낙폭2‘의 값을 고점값 115로 나눈 비율 $\frac{115-105}{115}=약 9\%$를 MDD라고 한다.

\[{MDD(최대 손실율)} = \frac{고점값 - 저점값}{고점값} = \frac{최대낙폭값}{고점값}\]

import numpy as np

def MDD(price):
    try:
        저점인덱스 = np.argmax(np.maximum.accumulate(price) - price)
        고점인덱스 = np.argmax(price[:저점인덱스])
        mdd = ((price[고점인덱스] - price[저점인덱스]) / price[고점인덱스])
        return 저점인덱스, 고점인덱스, mdd
    except:
        return np.nan, np.nan, np.nan


# 월 별 평가금액
price = [100, 110, 105, 115, 105, 110]
# MDD
mdd = MDD(price)[2]

print(f"{mdd*100:.0f}%")

9%

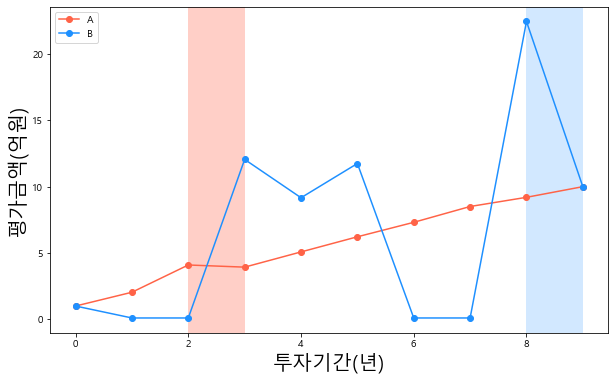
예를 들어, A와 B가 각각 1억 원 씩 투자해 10년 후 모두 10억 원으로 불렸다고 가정해보자. A의 경우 4년 차에 MDD 4%를 제외하고 추가적인 낙폭없이 꾸준히 상승해 10년 차에 10억 원이 되었고, B의 경우 9년 차에 22억 까지 가파르게 오른 뒤 10년 차에 10억으로 떨어져 MDD 55%를 기록했다고 생각해보자. A, B 둘 모두 10년 만에 자산을 10배 수준으로 불렸지만, B는 A보다 손실에 대한 심리적 고통을 더 크게 느낄 가능성이 높다고 볼 수 있다. 심지어 투자 기간 도중에 매우 큰 MDD를 기록했다면 심리적 고통이 큰 나머지 투자 행위 자체를 포기할 수도 있다.

import numpy as np
np.random.seed(18)

A = np.array(range(2, 10)) + np.random.normal(0, 0.5, 8)
A = np.append(1, A)
A = np.append(A, 10)
A[A < 0] = 0.1

B = np.array(range(2, 10)) + np.random.normal(0, 10, 8)
B = np.append(1, B)
B = np.append(B, 10)
B[B < 0] = 0.1

plt.figure(figsize=(10, 6))
plt.plot(A, marker='o', color='tomato', label="A")
plt.plot(B, marker='o', color='dodgerblue', label="B")
plt.legend()
plt.ylabel("평가금액(억원)", fontsize=20)
plt.xlabel("투자기간(년)", fontsize=20)

try:
    저점인덱스_a, 고점인덱스_a, mdd_a = MDD(A)
    plt.axvspan(저점인덱스_a, 고점인덱스_a, facecolor='tomato', alpha=0.3)
except:
    pass

try:
    저점인덱스_b, 고점인덱스_b, mdd_b = MDD(B)
    plt.axvspan(저점인덱스_b, 고점인덱스_b, facecolor='dodgerblue', alpha=0.2)
except:
    pass
plt.show()

print(f"""
A의 MDD: {mdd_a * 100:.0f}%
> 고점값: {A[고점인덱스_a]:.1f}억 원
> 저점값: {A[저점인덱스_a]:.1f}억 원
B의 MDD: {mdd_b * 100:.0f}%
> 고점값: {B[고점인덱스_b]:.1f}억 원
> 저점값: {B[저점인덱스_b]:.1f}억 원
""")

A의 MDD: 4%
> 고점값: 4.1억 원
> 저점값: 3.9억 원
B의 MDD: 55%
> 고점값: 22.5억 원
> 저점값: 10.0억 원

참고

• 할 수 있다! 퀀트 투자 - 강환국 저